If there are
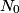 muons at time muons at time 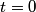 , then at some later time , then at some later time 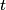 , there would be , there would be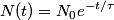 So, at time 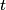 , the muons decay at a rate , the muons decay at a rate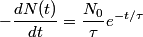 So, in a time interval 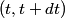 , , 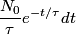 muons decay. So, the probability that a muon decays in this time interval is 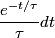 A muon that travels a distance 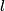 in the laboratory will decay at time in the laboratory will decay at time 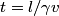 in its rest frame. in its rest frame. 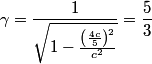 So, 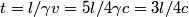 . So, the probability that a muon decays after traveling a distance . So, the probability that a muon decays after traveling a distance 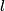 is is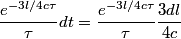 The mean distance traveled by the muons is therefore, ![\begin{align*}\int_0^{\infty}l\frac{ e^{ -3l/4c\tau}}{\tau}\frac{3dl}{4c}\\&= \left[-l e^{ -3l/4c\tau}\right]_0^{\infty} ... \begin{align*}\int_0^{\infty}l\frac{ e^{ -3l/4c\tau}}{\tau}\frac{3dl}{4c}\\&= \left[-l e^{ -3l/4c\tau}\right]_0^{\infty} ...](../images/d81fa6dd7a619e7b9f4a3c3b84fa985c23a23d49.gif) Plugging in 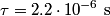 and and 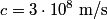 gives gives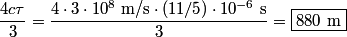 Therefore, answer (C) is correct. |